If you have ever taken a course in probability you have likely heard of the ‘Monty Hall Problem’, based on the name of the host of the show ‘Let’s Make a Deal’. On my current work project this week someone on the technical team inadvertantly offered such a choice without knowing or understanding it … which turned into a fun education for the non-statisticians on the team.
The setup is this: you have a free choice between three items (on the show they were doors, and a prize was behind one). One is correct and the other two are incorrect. If you ask people what the chances are of choosing correctly at this point they will generally be correct in answering ‘1 out of 3’ or 33%.
But what happens next? Monty opens one of the remaining doors – one that he knows in advance does NOT have the prize. You are then offered a choice – stick with your current choice or switch.
What should you do?
For most people the answer is ‘No’. Why? The thought is that there is now a 50% chance of each door having the prize, so the bias goes to your original choice.
Sounds very reasonable, right? Two doors, one prize … 50%. Only problem? It is wrong! You absolutely SHOULD switch!
What? How does this work? Let’s take a look …
When you are first choosing, each choice has a 33% chance of being correct. That means if you choose #1, there is a 66% chance you are wrong – in other words, there is a 66% chance it is #2 or #3. The way to think about this is that yuo have a 1/3 chance of being correct and a 2/3 chance of being incorrect. This much is obvious.
But when Monty reveals that it is NOT #2, he does NOT change the denominator of the equation – there are STILL 3 possibilities! And that is where people get confused. So you have your initial choice with 1/3 possibility of being correct, the door Monty revealed which now has a 0/3 chance of being correct … and the final door which has a 2/3 chance of being the right one!
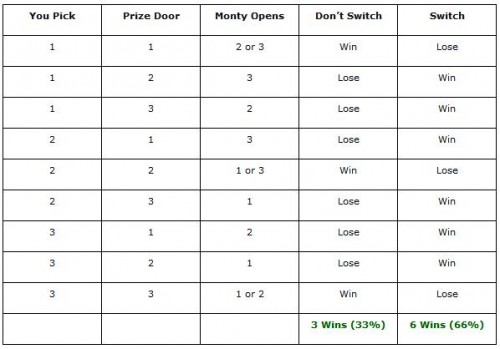
In other words, once Monty reveals the losing door, you are TWICE as likely to get a prize by switching! Still not convinced? Take a look at this table from the Minitab blog:
What is YOUR favorite math or probability or physics problem that stumps people?
Source: Minitab Blog


Here’s another way to understand the result: If you originally picked the prize and you switch, you’ll end up without the prize. On the other hand, if you originally didn’t pick the prize and you switch, you will end up with the prize. If you switch, a good choice becomes a bad choice, and a bad choice becomes a good choice. Since the original probability of making a bad choice was 2/3, the probability that you’ll get the prize if you switch is 2/3.
Sorry, that table is incorrect in determining all possibilities.
You can’t merely use the “2 or 3”, “1 or 3”, and “1 or 2” lumped together. You have to consider them separately.
For example, when you lump together the scenario where you have chosen the correct door, say door #1, you have to consider Monty’s selection of opening door #2 or door #3 as separate situations; lumping them together is what causes a perception that switching increases the odds of winning.
That table correctly formulated for all situations would read:
Your selection………..Correct……….Reveal………….Keep………Switch
……….1…………………….1…………………2……………..Win………….Lose
……….1…………………….1…………………3……………..Win………….Lose
……….1…………………….2…………………3……………..Lose………..Win
……….1…………………….3…………………2……………..Lose………..Win
And so on. The odds are still 50/50
Yes but not all situations are equally likely: situations 1 and 2 occur 1/6 each, and 3 and 4 occur 1/3 each. Therefore 2/3 times switching wins.
Exactly. This solution isn’t up for debate at this point … it is a fairly old thing that has been rigorously proved. Many top-name mathematicians had the same first (incorrect) instinct.